OTHER CLASS XII TOPICS
Application of Integrals
Applications of Derivatives
Continuity and Differentiability
Integration
Matrices
Probability
Relations and Functions
Three Dimensional Geometry
Trigonometry
Vector Algebra
Default
Mathematics Class XII Application of Integrals Finding the area bounded by a curve
Question
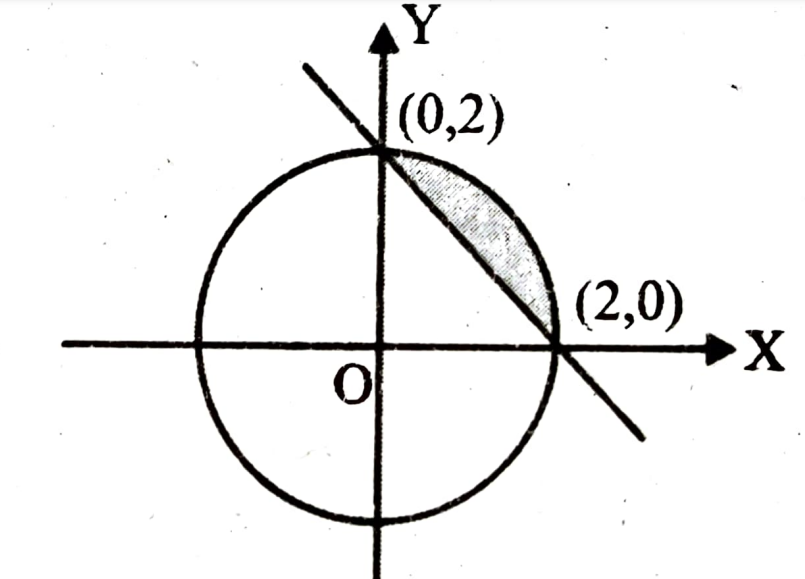
Find the smaller area enclosed by the circle $x^2 + y^2 = 4$ and the line $x + y = 2$
34fd3ee1-7639-11ed-94f3-5405dbb1cb03