Quotient = $x - 3$
Remainder = $7x - 9$



(ii) $p(x)= x^{4}-3x^{2}+4x+5$, $g(x)= x^{2}+1-x$

Quotient = $x^2+x-3$
Remainder = $8$



(iii) $p(x)= x^{4}-5x+6$, $g(x)= 2-x^{2}$

Quotient = $-x^2-2$
Remainder = $-5x+10$

---

2

Check whether the first polynomial is a factor of the second polynomial by dividing the second polynomial by the first polynomial.

(i) $t^2 - 3$, $2t^4 + 3t^3 - 2t^2 - 9t - 12$
(ii) $x^2 + 3x + 1$, $3x^4 + 5x^3 - 7x^2 + 2x + 2$
(iii) $x^2 + 3x + 1$, $x^5 - 4x^3 + x^2 + 3x + 1$

Solution

(i) $t^2-3$, $2t^4 + 3t^3-2t^2-9t-12$

As the remainder is zero, first polynomial is a factor of second polynomial.



(ii) $x^2 + 3x + 1$, $3x^4 + 5x^3-7x^2 + 2x + 2$

As the remainder is zero, first polynomial is a factor of second polynomial.



(iii) $x^3 - 3x + 1$, $x^5-4x^3 + x^2 + 3x + 1$

As the remainder is not zero, first polynomial is not a factor of second polynomial.

---

3

Obtain all other zeroes of $3x^4 + 6x^3-2x^2-10x-5$, if two of its zeroes are $\sqrt { \frac { 5 }{ 3 } }$ and -$\sqrt { \frac { 5 }{ 3 } }$.

Solution

Let $p(x) =$ $3x^4 + 6x^3-2x^2-10x-5$
The given zeroes are $\sqrt { \frac { 5 }{ 3 } }$ and -$\sqrt { \frac { 5 }{ 3 } }$

Hence $\left(x - \sqrt { \frac { 5 }{ 3 } }\right)$ $\left(x + \sqrt { \frac { 5 }{ 3 } }\right)$ = $\left(x^2 - \dfrac{5}{3}\right)$ is a factor.

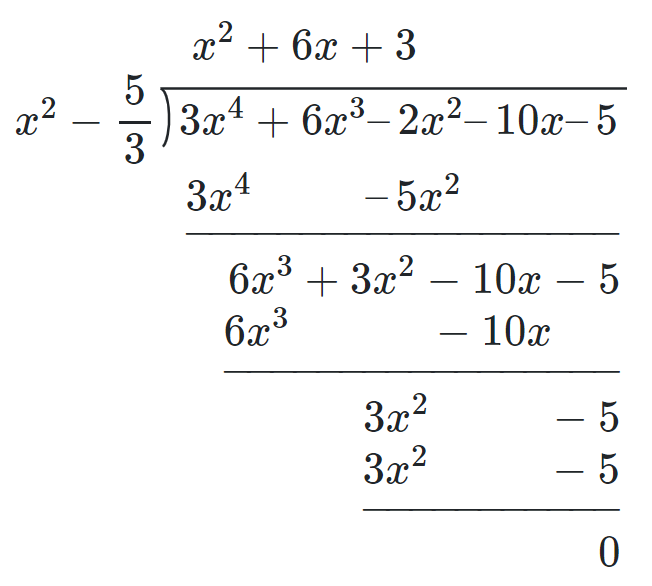
Dividing $3x^4 + 6x^3-2x^2-10x-5$ by $\left(x^2 - \dfrac{5}{3}\right)$, we get $3x^2 + 6x + 3$
Let us factorize $3x^2 + 6x + 3$
$3x^2 + 6x + 3$
$ ⇒ 3x^2 + 3x + 3x + 3$
$ ⇒ 3x(x + 1) + 3(x + 1)$
$ ⇒ 3(x + 1)(x + 1)$
$∴ p(x) =$ $3\left(x^2 - \dfrac{5}{3}\right)(x + 1)(x + 1)$
∴ The other 2 zeroes are -1 and -1

---

4

On dividing $x^{3}-3x^{2}+x+2$ by a polynomial g(x), the quotient and remainder were $x-2$ and $-2x+4$ repectively. Find g(x)

Solution

Quotient × Divisor + Remainder = Dividend
$∴ (x - 2) × g(x) + (-2x + 4)$ = $x^{3}-3x^{2}+x+2$
$⇒ (x - 2) × g(x)$ = $x^{3}-3x^{2}+x+2 + 2x - 4$

$∴ g(x)$ = $\dfrac{x^{3}-3x^{2}+3x-2}{x - 2}$

$∴ g(x)$ = $x^2 - x + 1$

---

5

Give examples of polynomials p(x), g(x), q(x) and r(x), which satisfy the division algorithm and

(i) deg p(x)= deg q(x) (ii) deg q(x)= deg r(x) (iii) deg r(x)=0

Solution

According to Euclid's division lemma,
$p(x) = g(x) × q(x) + r(x)$ where $q(x) ≠ 0$

(i) Degree of quotient will be equal to degree of dividend when divisor is constant (degree is 0).
Let us consider the division of $8x^2 + 4x + 9$ by 4.
Here, $p(x) = 8x^2 + 4x + 9$ and $g(x) = 4$
$⇒ q(x) = 2x^2 + x + 2$ and $r(x) = 1$

Therefore, degree of p(x) and q(x) is same which is 2.


(ii) Let us consider the division of $2x^2 + 4x + 7$ by $x^2 + 2x + 1$,
Here, $p(x) = 2x^2 + 4x + 7$ and $g(x) = x^2 + 2x + 1$

Therefore, $q(x) = 2$ and $r(x) = 5$


(iii) Degree of remainder will be 0 when remainder obtained on division is a constant.
Let us consider the division of $10x^3 + 3$ by $5x^2$.
Here, $p(x) = 10x^3 + 3$ and $g(x) = 5x^2$
$q(x) = 2x$ and $r(x) = 3$

Therefore, the degree of $r(x)$ is 0.