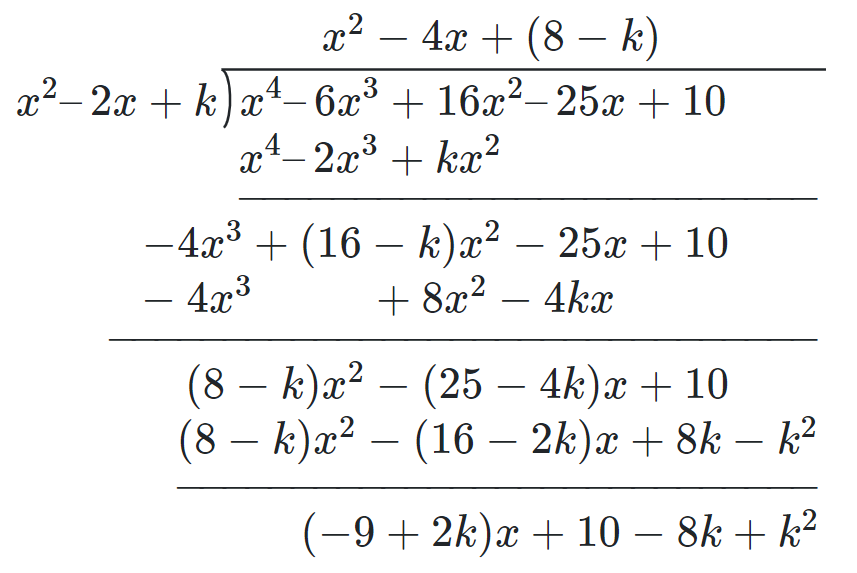Vachmi
Verify that the numbers given alongside of the cubic polynomials below are their zeroes.
Also, verify the relationship between the zeroes and the coefficients in each case:
(i) $2x^3 + x^2-5x + 2; \frac { 1 }{ 2 }, 1, -2$
(ii) $x^3-4x^2 + 5x-2; 2, 1, 1$
Solution
(i) On comparing the given polynomial with the polynomial $ax^3 + bx^2 + cx + d$,
we obtain a = 2, b = 1, c = -5, d = 2
∴ p(x)= $2x^{3}+x^{2}-5x+2$
$p\left(\dfrac{1}{2}\right)= 2\times \left(\dfrac{1}{2}\right)^{3}+\left ( \dfrac{1}{2} \right )^{2}-5\left ( \dfrac{1}{2}\right ) +2$
$ = \dfrac{1}{4}+\dfrac{1}{4}-\dfrac{5}{2}+2= 0$
$p(1)= 2\times 1^{3}+1^{2}-5(1)+2$
= $2+1-5+2$ = $0$
$p(-2)= 2(-2)^{3}+(-2)^{2}-5(-2)+2$
$= -16+4+10+2=0$
Hence $\dfrac{1}{2}$, 1 and -2 are the zeroes.
α = $\dfrac{1}{2}$, β = 1, γ= -2
α+β+γ = $-\dfrac{1}{2}$ = $\dfrac{b}{a}$
αβ+βγ+γα = $-\dfrac{5}{2}$ = $\dfrac{c}{a}$
αβγ = $-\dfrac{2}{2}$ = $-\dfrac{d}{a}$
Thus, the relationship between the zeroes and the coefficients is verified.
(ii) On comparing the given polynomial with the polynomial $ax^3 + bx^2 + cx + d$,
we obtain a = 1, b = -4, c = 5, d = -2.
$∴ p(x)= x^{3}-4x^{2}+5x-2$
$p(2)= 2^{3}-4(2)^{2}+5(2)-2$
$=8-16+10-2=0$
$p(1)= 1^{3}-4(1)^{2}+5(1)-2= 0$
Hence 2, 1 and 1 are the zeroes.
α= 2 β = 1 γ= 1
α+β+γ = $\dfrac{4}{1}=\dfrac{-b}{a}$
αβ+βγ+γα = $\dfrac{5}{1}= \dfrac{c}{a}$
αβγ = $\dfrac{2}{1}= -\dfrac{d}{a}$
Thus, the relationship between the zeroes and the coefficients is verified.
2
Find a cubic polynomial with the sum, sum of the product of its zeroes taken two at a time, and the product of its zeroes as 2, -7, -14 respectively.
Solution
Let the zeroes of the required polynomial be α, β, γ.
∴ α+β+γ = 2 and
αβ+βγ+γα = -7 and
αβγ = -14
The cubic polynomial is of the form
$x^3$ - (sum of the zeros) $x^2$ + (sum of the product of the zeros taken two at a time) - (product of the zeros) = 0
$⇒ x^3 - (α+β+γ)x^2 + (αβ+βγ+γα)x - (αβγ)$ $= 0$
$⇒ x^3 -2x^2-7x+14=0$ is the required polynomial.
3
If the zeroes of the polynomial $x^3-3x^2 + x + 1$ are a-b, a, a + b, find a and b.
Solution
Let α, β, and γ be the zeroes of equation $p(x) = x^3 - 3x^2 + x + 1$
The zeroes of the polynomial p(x) are given as a - b, a, a + b.
∴ Sum of the zeroes = α+β+γ = 3=(a-b)+a+(a+b)
∴ 3a=3 or a=1............(i)
Product of the zeroes αβγ = -1=(a-b)a(a+b)
$a^{3}-ab^{2}=-1$.........(ii)
Substituting the value of a from (i) and (ii), we get,
$1^{3}-1b^{2}=-1$
$b^{2}=2$ or $b = \sqrt{2}$
Hence $a=1$ and $b=\sqrt{2}$
4
If two zeroes of the polynomial $x^4 - 6x^3 - 26x^2 + 138x - 35$ are $2 ± \sqrt{3}$, find other zeroes.
Solution
The 2 zeroes which are given are $2+ \sqrt{3}$ and $2-\sqrt{3}$
$∴ \left (x-(2+\sqrt{3}) \right) \left(x-(2-\sqrt{3}) \right)$
$= (x-2)^{2}-(\sqrt{3})^{2}$
Therefore, $x^2 - 4x + 1$ is a factor of the given polynomial.
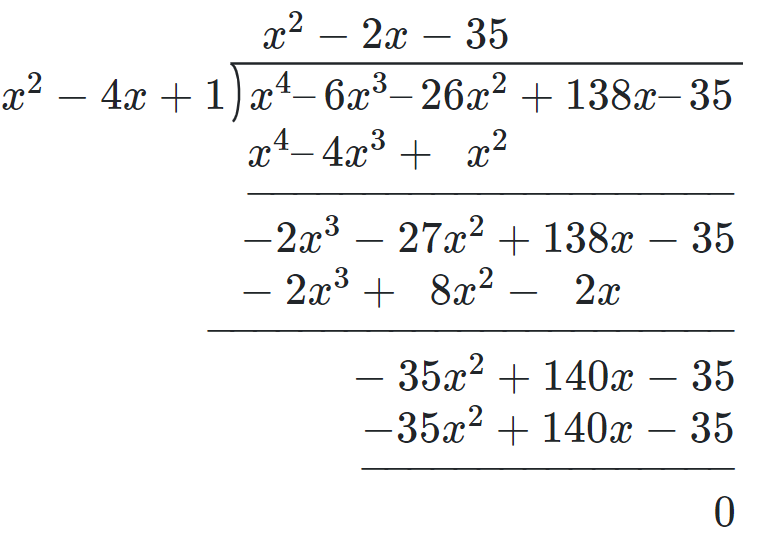
So $x^4 - 6x^3 - 26x^2 + 138x - 35$
$= (x^{2}-4x+1)(x^2-2x-35)$
$= (x^{2}-4x+1)(x^2-7x+5x-35)$
$= (x^{2}-4x+1)(x(x-7)+5(x-7))$
$= (x^{2}-4x+1)(x-7)(x+5)$
Hence the other zeroes of the polynomial are 7 and -5
If the polynomial $x^4 - 6x^3 + 16x^2 - 25x + 10$ is divided by another polynomial $x^2 - 2x + k$, the remainder comes out to be $x + a$, find $k$ and $a$.
Solution
$p(x) = x^4 - 6x^3 + 16x^2 - 25x + 10$
Dividing by $x^2 - 2x + k$,